Tests of special relativity
Special relativity is a physical theory that plays a fundamental role in the description of all physical phenomena, as long as no considerable influence of gravitation occurs. Many experiments played (and still play) an important role in its development and justification and the strength of the theory lies in the fact that it is the only one that can correctly predict to high precision the outcome of all known (and very different) experiments. Many of those experiments are still conducted with increased precision and the only area where deviations of the predictions of special relativity are not completely ruled out by experiment is at the Planck scale and below. Collections of various tests on special relativity were given by Jakob Laub,[1] Zhang,[2] Mattingly,[3] Clifford Will,[4] and Roberts/Schleif.[5]
Special relativity is restricted to flat spacetime, i.e., to all phenomena without significant influence of gravitation. The latter lies in the domain of general relativity and the corresponding Tests of general relativity must be considered.
Contents |
Refutations of the aether
The predominant theory of light in the 19th century was that of the luminiferous aether, a stationary medium in which light is propagating like sound is propagating in air. From that it follows that the speed of light is constant in all directions in the aether and is independent of the velocity of the source. Thus an observer moving relative to the aether must consequently measure some sort of "aether wind" as an observer moving relative to air measures an apparent wind.
First-order experiments
A series of optical experiments were conducted, which should have given a positive result for magnitudes to first order in 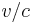 and thus demonstrating the relative motion of the aether. Yet the results were negative. This problem was solved by Augustin Fresnel (1818) by the introduction of an auxiliary hypothesis, the so called "dragging coefficient", that is, matter is dragging the aether to a small extent. This coefficient was directly demonstrated by the Fizeau experiment (1851) and it was later shown that all optical experiments must give a negative result due to this coefficient.[1]
and thus demonstrating the relative motion of the aether. Yet the results were negative. This problem was solved by Augustin Fresnel (1818) by the introduction of an auxiliary hypothesis, the so called "dragging coefficient", that is, matter is dragging the aether to a small extent. This coefficient was directly demonstrated by the Fizeau experiment (1851) and it was later shown that all optical experiments must give a negative result due to this coefficient.[1]
Also, some electrodynamic experiments were conducted whose negative result cannot be explained by Fresnel's theory. Thus Hendrik Lorentz (1892, 1895) was forced to introduce several new auxiliary variables for moving observers. For example, a location-variable by which electrostatic fields contract in the line of motion and another variable ("local time") by which the time coordinates for moving observers depend on their current location.
Second-order experiments
The stationary aether theory, however, would give positive results when the experiments are precise enough to measure magnitudes of second order in 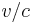 . The first experiment of this kind was the Michelson–Morley experiment (1881, 1887) where two rays of light, traveling for some time in different directions were brought to interfere so that different orientations relative to the aether should lead to a displacement of the interference fringes. But the result was negative again. The only way out of this dilemma was to assume that matter is contracted in the line of motion with respect to the aether (length contraction, by George Francis FitzGerald (1889) and Lorentz (1892)). That is, the older hypothesis of a contraction of electrostatic fields was extended to intermolecular forces. However, since there was no theoretical reason for that, the contraction hypothesis was considered ad hoc.
. The first experiment of this kind was the Michelson–Morley experiment (1881, 1887) where two rays of light, traveling for some time in different directions were brought to interfere so that different orientations relative to the aether should lead to a displacement of the interference fringes. But the result was negative again. The only way out of this dilemma was to assume that matter is contracted in the line of motion with respect to the aether (length contraction, by George Francis FitzGerald (1889) and Lorentz (1892)). That is, the older hypothesis of a contraction of electrostatic fields was extended to intermolecular forces. However, since there was no theoretical reason for that, the contraction hypothesis was considered ad hoc.
Besides the optical Michelson–Morley experiment, its electrodynamic equivalent was also conducted, the Trouton–Noble experiment. By that it should be demonstrated that a moving condenser must be subjected to a torque. Again, the result was negative. Then it an attempt was also made to measure some consequences of length contraction in the laboratory frame, since it was assumed that it would lead to birefringence – again the results were negative. (The Trouton–Rankine experiment conducted in 1908 also gave a negative result when measuring the influence of length contraction on a coil.)[1]
To explain all experiments conducted before 1904, Lorentz was forced to again expand his theory by introducing the complete Lorentz transformation. Henri Poincaré declared in 1905 that the impossibility of demonstrating absolute motion (principle of relativity) is apparently a law of nature.
Refutations of complete aether drag
The idea that the aether is completely dragged within or in the vicinity of earth, by which the negative aether drift experiments could be explained, was refuted by the experiments of Oliver Lodge (1893) by means of rotating disks; by Hammar (1935) by means of an interferometer with one arm enclosed by mercury while the other one was free; the Sagnac effect which showed that the velocity of two light rays is unaffected by the rotation of the platform; and the existence of the aberration of light. Also, the assumption that aether drag is proportional to mass and thus only occurs with respect to Earth as a whole was refuted by the Michelson–Gale–Pearson experiment, which demonstrated the Sagnac effect through Earth's motion.
Special relativity
Basic experiments
Eventually, Albert Einstein (1905) drew the conclusion that established theories and facts such as the following only form a logical coherent system when the concepts of space and time are subjected to a fundamental revision.
- Maxwell-Lorentz's electrodynamics (independence of the speed of light from the speed of the source)
- the negative aether drift experiments (no preferred reference frame)
- Moving magnet and conductor problem (only relative motion is relevant)
- the Fizeau experiment and the aberration of light (no complete aether drag)
The result is special relativity theory, which is based on the constancy of the speed of light in all inertial frames of reference and the principle of relativity. Here, the Lorentz transformation is not a mere collection of auxiliary hypotheses any more but reflects a fundamental Lorentz symmetry and forms the basis of successful theories such as Quantum electrodynamics. Special relativity offers a large number of testable predictions, such as:[6]
| Principle of relativity | Constancy of the speed of light | Time dilation |
|---|---|---|
| Any uniformly moving observer in an inertial frame cannot determine his "absolute" state of motion by a co-moving experimental arrangement. | In all inertial frames the measured speed of light is equal in all directions (isotropy), independent of the speed of the source, and cannot be exceeded by moving bodies. | The rate of a clock C (= any periodic process) traveling between two synchronized clocks A and B at rest in an inertial frame is retarded with respect to the two clocks. |
| Also other relativistic effects such as length contraction, Doppler effect, aberration and the experimental predictions of relativistic theories such as the Standard Model can be measured. | ||
The effects of special relativity can phenomenologically be derived from the following three types of experiments (besides these experiments, a large number of other types of experiments were, and still are, conducted):[3][5][7]
- Michelson–Morley experiment, by which the dependence of the speed of light on the direction of the measuring device can be tested.
- Kennedy–Thorndike experiment, by which the dependence of the speed of light on the velocity of the measuring device can be tested.
- Ives–Stilwell experiment, by which time dilation can be tested.
The combination of these effects is important since most of them can be interpreted in different ways when viewed individually. For example, isotropy experiments such as Michelson-Morley can be seen as a simple consequence of the relativity principle, according to which any inertially moving observer can consider himself as at rest. Therefore, it is also compatible to Galilean-invariant theories like emission theories or complete aether drag, which also contain some sort of relativity principle. Only by the addition of other experiments that exclude the Galilean-invariant theories (such as the Ives–Stillwell experiment or refutations of emission theories and complete aether drag) Lorentz-invariance and thus special relativity remains as the only theory that can explain all those experiments.
Isotropy of the speed of light
Interferometers, resonators, clock-comparison
To measure the isotropy of the speed of light variations of the Michelson-Morley and Kennedy-Thorndike experiments are still under way. Contrary to Michelson-Morley-, the Kennedy-Thorndike-experiments employ different arm lengths and the evaluations last several months. In that way, the influence of different velocities during Earth's orbit around the sun can be observed. In modern variants of Michelson-Morley and Kennedy-Thorndike, laser, maser and optical resonators are used reducing the possibility of any anisotropy of the speed of light to 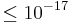 for Michelson-Morley and
for Michelson-Morley and 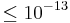 for Kennedy-Thorndike. Not only terrestrial tests are being conducted but also Lunar Laser Ranging Experiments as a variation of the Kennedy-Thorndike-experiment.[4]
for Kennedy-Thorndike. Not only terrestrial tests are being conducted but also Lunar Laser Ranging Experiments as a variation of the Kennedy-Thorndike-experiment.[4]
In addition, extremely precise clock-comparison experiments (because periodic processes and frequencies can be considered as clocks) such as the Hughes–Drever experiments are also still conducted. They are not restricted to the photon sector as Michelson-Morley but directly determine any anisotropy of mass by measuring the ground state of nuclei. In other words, they determine the anisotropy of space providing an upper limit of such anisotropies of 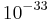 GeV. Thus they belong to the most precise measurements at all.[3][4]
GeV. Thus they belong to the most precise measurements at all.[3][4]
Another type of isotropy experiments are the Moessbauer rotor experiments in the 1960s, by which the anisotropy of the Doppler effect on a rotating disc can be observed by using the Moessbauer effect (those experiments can also utilized to measure time dilation, see below).
No dependence on source velocity or energy
Emission theories, according to which the speed of light depends on the velocity of the source, can explain the negative outcome of the aether drift experiments as well. However, a series of experiments definitely ruled out these models. For example, the Alväger–Experiment where the photons don't acquire the speed of the decaying mesons; the Sagnac experiment in which the light rays are moving independently of the velocity of the rotating apparatus; the de Sitter double star experiment showing that the orbits of the stars don't appear scrambled due to different propagation times of light.
Other observations also demonstrated that the speed of light is independent of the frequency and energy of the light rays.[3]
One-way speed of light
A series of one-way measurements were undertaken, all of them confirming the isotropy of the speed of light.[5] However, it is to be noticed that only the two-way speed of light (from A to B back to A) can directly be measured since the one-way speed depends on the definition of simultaneity and therefore on the method of synchronization. The Poincaré-Einstein synchronization makes the one-way speed equal to the two-way speed, yet one can think of other synchronizations, which also give a isotropic two-way speed but an anisotropic one-way speed. It was also shown that synchronization by slow clock transport is equivalent with Einstein synchronization and also non-standard synchronization as long as the moving clocks are subjected to time dilation. Now, because the one-way speed is depending on the definition of simultaneity, only the two-way speed is directly accessible by experiment so there are many models with anisotropic one-way speed of light that are experimentally equivalent to special relativity. However, from all of these only special relativity is acceptable for the overwhelming majority of physicists since all other synchronizations are much more complicated than Einstein's one, and because the other models (like Lorentz ether theory) are based on extreme and implausible assumptions concerning some dynamical effects, which are aimed at hiding the "preferred frame" from observation.
Time dilation and Length contraction
The transverse Doppler effect, and thus time dilation, was directly observed in the Ives–Stilwell experiment (1938) for the first time, where the displacement of the center of gravity of the overlapping light waves was evaluated. In modern Ives-Stilwell experiments in heavy ion storage rings using saturated spectroscopy the maximum deviation from time dilation was limited to 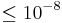 . Another variant is the Moessbauer rotor experiment in which gamma rays were sent from the middle of a rotating disc to a receiver at the edge of the disc so that the transverse Doppler effect can be evaluated by means of the Moessbauer effect. By measuring the lifetime of muons in the atmosphere and in particle accelerators the time dilation of moving particles was also verified. On the other hand, the Hafele–Keating experiment confirmed the twin paradox, i.e. that a clock moving from A to B back to A is retarded with respect to the initial clock. However, in this experiment the effects of general relativity also play an essential role.
. Another variant is the Moessbauer rotor experiment in which gamma rays were sent from the middle of a rotating disc to a receiver at the edge of the disc so that the transverse Doppler effect can be evaluated by means of the Moessbauer effect. By measuring the lifetime of muons in the atmosphere and in particle accelerators the time dilation of moving particles was also verified. On the other hand, the Hafele–Keating experiment confirmed the twin paradox, i.e. that a clock moving from A to B back to A is retarded with respect to the initial clock. However, in this experiment the effects of general relativity also play an essential role.
Direct confirmation of length contraction is hard to achieve in practice since the dimensions of the observed particles are vanishingly small. However, there are indirect confirmations; for example, the behavior of colliding heavy ions can only be explained if their increased density due to Lorentz contraction is considered. Contraction also leads to an increase of the intensity of the Coulomb field perpendicular to the direction of motion whose effects already have been observed. Consequently, both time dilation and length contraction must be considered when conducting experiments in particle accelerators.
Relativistic mass and energy
Starting with 1901, a series of measurements was conducted aimed at demonstrating the velocity dependence of the mass of cathode rays. The results actually showed such a dependency but the precision necessary to distinguish between competing theories was disputed for a long time. Eventually, it was possible to unambiguously rule out all competing models except special relativity.
Today, special relativities predictions are routinely confirmed in particle accelerators such as the Relativistic Heavy Ion Collider. For example, the increase of relativistic momentum and energy is not only precisely measured but also necessary to understand the behavior of cyclotrons and synchrotrons etc., by which particles are accelerated near to the speed of light.
Sagnac and Fizeau
Special relativity also predicts that two light rays traveling in opposite directions around a loop or closed path require different flight times to come back to the moving emitter/receiver (this is a consequence of the independence of the speed of light from the velocity of the source, see above). This effect was actually observed and is called the Sagnac effect. Today the consideration of this effect is necessary for many experimental setups and for the correct functioning of GPS.
If such experiments are being conducted in moving media it is also necessary to consider Fresnel's dragging coefficient as demonstrated by the Fizeau experiment. Although this effect was initially understood as giving evidence of a nearly stationary aether or a partial aether drag it can easily be explained with special relativity by using the velocity composition law.
Test theories
Several test theories have been developed to assess a possible positive outcome in Lorentz violation experiments by adding certain parameters to the standard equations. These include the Robertson-Mansouri-Sexl framework (RMS) and the Standard-Model Extension (SME). RMS has three testable parameters with respect to length contraction and time dilation. From that, any anisotropy of the speed of light can be assessed. On the other hand, SME includes many Lorentz violation parameters, not only for special relativity, but for the Standard model and General relativity as well, thus it has a much larger number of testable parameters.
Other modern tests
Due to the developments concerning various models of Quantum gravity in recent years deviations of Lorentz invariance (possibly following from those models) are again the target of experimentalists. Because "local Lorentz invariance" (LLI) also holds in freely falling frames experiments concerning the weak Equivalence principle belong to this class of tests as well. The outcomes are analyzed by test theories (as mentioned above) like RMS or, more importantly, by SME.[3]
- Besides the mentioned variations of Michelson–Morley and Kennedy–Thorndike experiments, Hughes–Drever experiments are also continued for isotropy tests in the proton and neutron sector.
- To detect possible deviations in the electron sector, spin-polarized Torsion balances are used.
- Time dilation is confirmed by observation of the Doppler effect of Lithium and those experiments are valid in the electron, proton, and photon sector.
- Other experiments use Penning traps to observe deviations of cyclotron motion and Larmor precession in electrostatic and magnetic fields.
- Possible deviations from CPT symmetry (whose violation represents a violation of Lorentz invariance as well) can be determined in experiments with neutral mesons, Penning traps and muons.
- Also observations in the Higgs sector are under way.
- Astronomical tests are conducted in connection with the flight time of photons, where Lorentz violating factors could cause anomalous dispersion and birefringence leading to a dependency of photons on energy, frequency or polarization.
- With respect to Threshold energy of distant astronomical objects, Lorentz violations could lead to alterations in the standard values for the processes following from that energy.
- Other candidates for astronomical observations are synchrotron radiation and Neutrino oscillations. Also, Airy disks are investigated to find possible deviations of Lorentz invariance that could drive the photons out of phase.
See also
|
|||||||||||||||||||||||
References
- ^ a b c Laub, Jakob (1910). "Über die experimentellen Grundlagen des Relativitätsprinzips". Jahrbuch der Radioaktivität und Elektronik 7: 405–463.
- ^ Zhang, Yuan Zhong (1997). Special Relativity and Its Experimental Foundations. World Scientific. ISBN 9789810227494.
- ^ a b c d e Mattingly, David (2005). "Modern Tests of Lorentz Invariance". Living Rev. Relativity 8 (5). http://www.livingreviews.org/lrr-2005-5.
- ^ a b c Will, C.M (2006). "Special Relativity: A Centenary Perspective". In T. Damour, O. Darrigol, B. Duplantier und V. Rivasseau. Poincare Seminar 2005. Basel: Birkhauser. pp. 33–58. arXiv:gr-qc/0504085.
- ^ a b c Roberts, T; Schleif, S; Dlugosz, JM (ed.) (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SR/experiments.html. Retrieved 2010-10-31.
- ^ Lämmerzahl, C. (2005). "Special Relativity and Lorentz Invariance". Annalen der Physik 517 (1): 71–102. Bibcode 2005AnP...517...71L. doi:10.1002/andp.200410127.
- ^ Robertson, H. P. (1949). "Postulate versus Observation in the Special Theory of Relativity". Reviews of Modern Physics 21 (3): 378–382. Bibcode 1949RvMP...21..378R. doi:10.1103/RevModPhys.21.378.